Your everyday world from a physicist's perspective
Necklaces and square wheels
Some time ago I was having tea with some friends. And while the conversation went on, my hands were playing with the tea boxes that were on the table. Then someone posed the question: suppose that we stack the boxes in such a way that each box sticks out a bit over the box below it, then how much could we let the top box stick out over the bottom box? Is there some kind of limit?
If I remember correctly we had only a few boxes at the time, and we didn't manage to get the top box to stick out more than about 3/4 box length over the bottom one. Some even argued that the absolute limit would be one box length (irrespective of the number of boxes).
Back home I looked into it more carefully and conducted some additional experiments. I didn't have tea boxes, so I used Lego bricks instead (see figure 1).

Clearly the proposed limit of 1 brick length does not hold (as the top blue brick is sticking out about 1.3 bricks over the bottom one). Then, what is the limit?
The theory of stacking
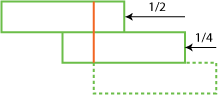
Let's start with the simplest case: two blocks. In this case it might be clear intuitively that the best we can do is to have the top block stick out about half a block length (see figure 2).

Now we have to think about it a bit. Why does the top block tilt over when it sticks out more than half a block length? The only downward force that acts on the top block is the force of gravity. In an uniform gravitational field (like locally near the surface of the earth) this gravitational force can be written as
(1)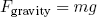 .
.
where g is the local gravitational acceleration (g ~ 9.8 in most places) and m is the amount of mass. The block will start to tilt when the downward force on the unsupported part is bigger than the downward force on the part supported by the bottom block. Since the mass of a Lego brick is distributed quite uniformly, the condition that the "tilting" force is equal to the "holding back" force is met when the block is exactly halfway.
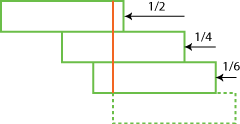
Suppose we are now trying to "stack" a third block below the two we have already in place. Where should we place it in order to have the two-block combination stick out as far as possible? Again we have to make sure that the supported mass to the right of the turning point is equal to the unsupported mass to the left. Figure 3 shows how this can be done.
Adding a fourth block below is a bit harder, but after some puzzling we can find the stable configuration shown in figure 4. One can easily check that the mass (i.e. the surface in the side view) on the left of the turning point (orange line) is equal to the mass on the right.
If this was an IQ test, we would now get the question: what is the next number in the sequence? You would probably guess it is 1/8. And you are quite right. It turns out that the displacement Dn for the n'th block can be captured in the simple formula
(2)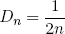 .
.
To find total overhang for N blocks we just have to sum Dn with n running from 1 to N,
(3)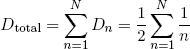 .
.
Now what if we make N very big? Will this sum converge to some finite value (since the thing we are adding becomes smaller and smaller) or will it keep on growing? If you ask a mathematician (or consult a book on calculus), he or she (or it, in case of the book) will tell you that it is the latter. There is no limit!
Finally, let us compare the theoretical optimal stacking (formula 2) with the overhang I could manage by carefully stacking my Lego bricks.
Not too bad I would say.
A story with a twist - the universal necklace shape
Now I would like to talk a bit about a phenomenon that is closely related to the stacking of bricks: a necklace or chain that is freely suspended between two fixed points (see figure 6).

One can find a formula for the shape of a suspended chain by using the general principle that objects in this world tend to come to rest in a state of minimal potential energy. This principle has of course everything to do with the fact that the entropy in the world tends to be a maximum.
Figure 7 shows a schematic of a chain of fixed length L suspended between the points x1 and x2.
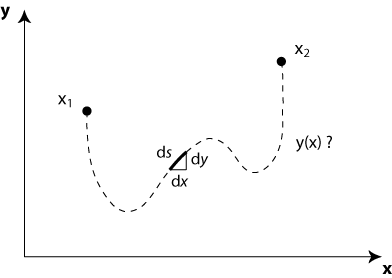
For an arbitrary shape y(x) the total potential energy can be written as the integral
(4)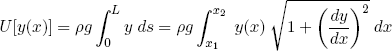 ,
,
where ρ is the mass per unit length of the chain and g is the gravitational constant. In the last step we used the fact that ds2 = dx2 + dy2 (Pythagoras' theory; see figure 7). U[y(x)] is a very special kind of function: it's a function of a function, also called a 'functional' by mathematicians. The mathematical problem now is to find the function y(x) for which the functional U[y(x)] takes its minimum value, given that its length has the fixed value L. This constraint of constant length can also be written in the form of a functional,
(5)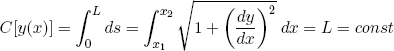 .
.
Luckily for us, the mathematics department (read Euler and Lagrange) came up with a general scheme to solve exactly this kind of problems (warning: this will be kind of advanced, skip to equation 12 if this all sounds like gibberish to you). They say that to find the function y(x) that minimizes U[y(x)] under the constraint that C[y(x)] = constant, one just needs to find the shape for which the composed functional
(6)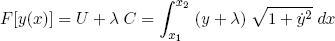 ,
,
has a minimum, where λ is some constant that has to be determined in the end. We cleaned up the notation a bit by replacing dy/dx by a y with a dot (also note that we removed the pre-factor ρg, as this will not change the shape for which the functional has a minimum).
For the time being we can get rid of the λ by making the simple coordinate transformation
(7)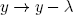 ;
;
we just have to remember to plug it back on in the end. Now comes the mathemagic. The Euler-Lagrange theorem states that, given any functional
(8)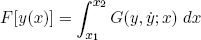 ,
,
the shape y(x) that minimizes (or maximizes) it, satisfies the differential equation
(9)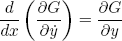 .
.
That's it. If we plug in our "G" from equation 6 we find, after a bit of labor (differentiating, product rules, chain rules, etc), the concise expression
(10)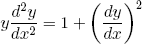 .
.
In other words: the shape y(x) we are looking for is a function for which the function itself times its second derivative, is equal to 1 plus its first derivative squared. After some research one will find that there exist just such a function. It's called the 'hyperbolic cosine' or 'cosh' and it reads
(11)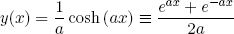 .
.
Tacking back on the constant λ, we find our final solution
(12)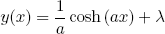 .
.
Here a is a parameter that can be used to (uniformly) adjust the size of the necklace shape and λ determines the vertical offset. With this simple formula we should be able to fit the shape of any freely suspended chain or necklace in the world! Let's put it to the test.

And to convince you of the claimed universality, here is another example.

The arch-necklace correspondence
At the beginning of this section I mentioned that the problem of the suspended necklace is closely related to the optimal overhang stacking of Lego bricks. To show this, I took the center points of the bricks calculated with equation 3 and tried to fit the curve of a flipped hyperbolic cosine to it. The result is plotted in figure 10.
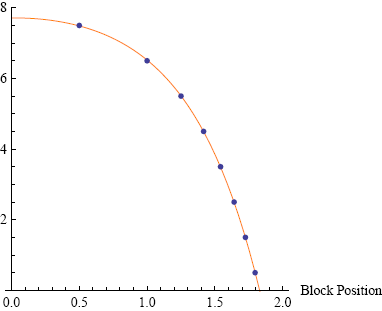
The correspondence is striking but not completely unexpected. The necklace problem is essentially the up-side-down version of the arch problem, with compression forces replaced by tension forces. Still it is interesting that such seemingly different approaches give the same answer.
Take-home message: if you ever want to build an arch that can safely support its own weight (or half an arch, like we did with the Lego bricks), one could simply use a piece of wire to find the appropriate shape (essentially using the wire as an analog calculator; I think this is what people did in the old days).
Bonus: square wheels
In geometry the hyperbolic cosine is often called a 'catenary' and can be defined as the curve that the locus of a parabola (i.e. the focus point of a parabolic mirror) traces out when the parabola is "rolled" over a line.
A funny geometrical property of the catenary curve is that when one rolls a line over it, there exists a point above this line (fixed with respect to the line) that traces out a horizontal line. This implies that one can design a road of catenary bumps on which a matched square (!) wheel can smoothly roll (see figure 11).
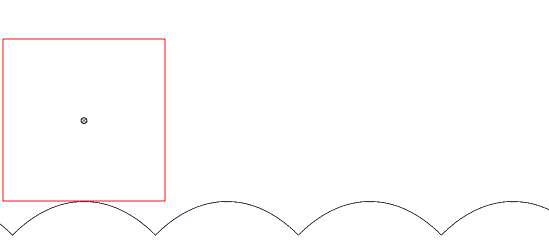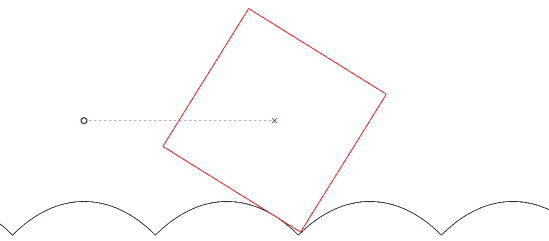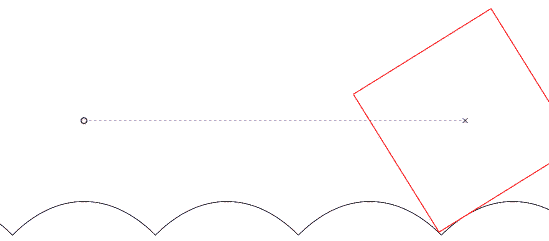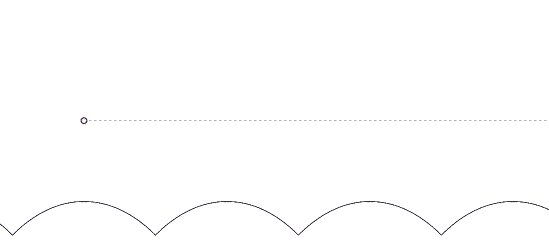
And of course people tried this.
Happy catenary spotting to y'all!
