Your everyday world from a physicist's perspective
Water bells
Some time ago a colleague of mine at the fluid lab showed me a wonderful little experiment, involving a water tap and a 1 euro coin.

When the water hits the coin, it first moves radially outward (as one would expect) and then smoothly curves back toward the central axis, forming a closed bell of streaming water (one has to experiment a bit with the water flow and the positioning of the coin to get a nice bell like the one shown above, but with some patience one can probably make an even bigger one!).
It turns out that this effect was already studied for the first time in 1833 by the famous French physicist Félix Savart and has fascinated many great physicist ever since (Boussinesq (1869), Taylor (1959) and, recently, Clanet (2001)). They found that the shape of the bell can be understood as an delicate interplay between inertia, surface tension and gravity. Below I will expand on their argument.
A question of shape
As Newton already noticed: objects always tend to keep on moving in the same way they did before (in straight lines, with constant velocity, that is). This is called the law of inertia and it is a very general law (although no-one knows why it is true). In order to speed something up, to slow something down or to make it go in a curve, one has to exert some kind of 'force' on the object. Newton used this idea to deduce the kind of "gravitational" force needed to make the planets go around the sun in elliptical orbits.
Physicists define the motion (or 'impulse') of an object by giving its total mass m (in kg) and three velocities measured in three orthogonal directions (which one can choose freely), say ux, uy and uz (in m/s). The rule by which a force changes the motion of an object in a small time dt can then be stated as
(1)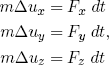 ,
,
where Fx, Fy, and Fz are the numerical values of the forces in the specified direction and the Δu's are the corresponding changes in velocity.
To make a particle deviate from its linear motion and let it move on a circular shaped path (like the water in our water bell), one needs a radially inward force that continuously changes the velocity perpendicular to its motion (see figure 1 below).
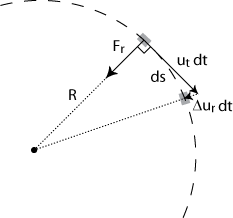
For small time steps dt we can deduce the following geometrical relation from this figure:
(2)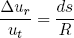 .
.
From our force rule (equation 1) we have
(3)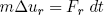 .
.
Solving equation 2 for Δur, plugging it in equation 3 and using that ut ≡ ds/dt we find
(4)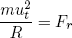 ,
,
which one might recognize as the centrifugal force rule. So now we know the inward force needed to make something with speed ut go on a circular path of radius R. However, we still have to figure out what supplies this force in the case of our water bell (as we have no small sun in there).
Surface tension
Water molecules stay together because they attract each other (otherwise they would move all over the place, like a gas). As a side effect of this attraction, the surface of the water acts like an elastic sheet (like a rubber balloon). If one pushes on the surface, the surface will bend a bit and then push back because it "wants" to be smooth (like a balloon full of air wants to remain balloon shaped). Because the 'surface tension' of water is a lot smaller than that of a balloon, only the smaller animals among us have direct experience with this effect (see figure 2).

Figure 3 below shows a schematic overview of the tension forces acting on a small piece of fluid in our water bell.
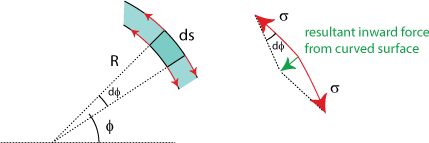
The force of surface tension always acts along the water surface (which means that it costs energy to stretch the surface). For water it is equal to a constant σ (that does depend on the temperature) times the width dw of the fluid particle perpendicular to the screen (not shown in figure 3, since I don't have a 3D screen). If the surface is curved, this tangential force will produce a net inward force, pulling the fluid particle to the center of its curved path. From figure 3 it is clear that this force can be written as
(5)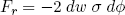 ,
,
or, by using some basic geometry, as
(6)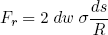 ,
,
The factor of two is in there because we have two surfaces. What cannot been seen in figure 3 is that the water sheet is also curved in the direction perpendicular to the screen (i.e. if one looks from above, the edge of the water bell traces out a circle). This produces an additional inward force equal to
(7)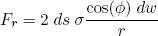 ,
,
where the small r is the distance measured from the central axis of the water bell, not to be confused with the big R which is the radius of curvature in the other direction.
Gravity
Another force we have to take into account is the force of gravity: the force that attracts everything toward the center of the earth. Now, everyone that has learned to walk, will have a great deal of direct experience with this force, so I won't dwell on it too much and just state that the inward force component on our piece of water (in figure 3) is given by
(8)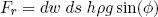 ,
,
where ρ is the density of water and g is the gravitational constant on earth (∼ 9.8 m/s2) and h is the thickness of the water sheet.
Putting it all together
Let's go back to our centrifugal force equation (equation 4) and plug in the sum of all the radial force components we found so far
(9)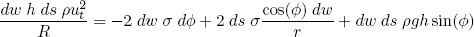 .
.
Dividing this equation by (dw ds) and noting that 1/R = -dφ/ds (geometry, figure 3) and dφ/ds = (dφ/dz) (dz/ds) (chain rule) = (dφ/dz) cos(φ) (geometry) we can write
(10)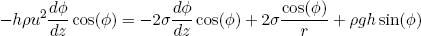 ,
,
where z is the position along the central axis (measured from the center of the coin downward).
The sheet thickness h can be related to the tangential velocity u and the distance from the vertical axis r via the conservation of water
(11)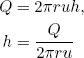 ,
,
where Q is the total flow rate from the water tap in liters per second (which can be measured with an measuring cup and a stopwatch).
Finally we can use the conservation of energy (gravitation energy mgz is converted to kinetic energy 1/2 mu2) to relate the velocity u(z) to the initial velocity u0 and the vertical position z
(12)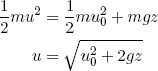 ,
,
so that the final equation (equation 10) reads
(13)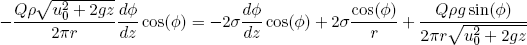 .
.
Together with the geometrical relation
(14)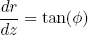 ,
,
we have a complete set of differential equations from which we can numerically solve r as a function of z, given an initial angle φ(0) and radial position r(0). Actually, Taylor succeeded to find an closed expression for this beast in the case that gravity is negligible, i.e. g = 0. He found that the bell then has a so called 'catenary' shape.
Since I'm not a genius (or a lazy genius at best), I let the mathematical software package Mathematica numerically solve this equation for me. Putting in the parameters Q, φ(0), r(0) and u0 I measured for my water bell, I find the following shape
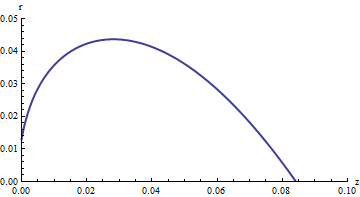
It looks very nice, but let's see how close it is to the real thing.

Now isn't that just beautiful! This is physics at its best. First collecting all the proper playing cards (inertia, surface tension, gravity and conservation of energy and matter in this case) and then carefully putting them together to build a complex card house that actually represents something one sees in the real world.
Fancy shapes
As one might recall from the previous article on tumbling books, a small perturbation can sometimes make a dynamic system go totally crazy. Lo and behold, and see what happens if you slowly decrease the flow rate after producing a stable bell (make sure that there are no holes in the sheet, or it won't work).

References
- Sir Geoffrey Taylor, The dynamics of thin sheets of fluid - I. Water bells, Proc. R. Soc. A 253, pp. 289-295 (1959)
- Christophe Clanet, Dynamics and stability of water bells, J. Fluid Mech. 430, pp. 111-147 (2001)
