Your everyday world from a physicist's perspective
Duck wakes
On a still day one can often observe ducks and other swimming animals decorate quiet ponds with beautiful patterns of waves.

In the spirit of Lord Kelvin, who gave a popular lecture on ship wakes in the Science and Art Museum in Edinburgh (Wednesday evening, 3rd August, 1887), I would like to describe how these patterns are formed. But before we come to the Kelvin wake pattern itself, we first have to know a few things about how waves travel on a water surface.
Water waves
An interesting way to see a water wave (also invented by Kelvin) is to imagine that we spread out a big flexible sheet over the water surface and then try to deform it as shown in figure 2. As you try this experiment (in your mind, or for real) you will notice that the water will push back on you as you try to make the dimples. This pressure is caused by the weight of the water and is called hydrostatic pressure. If you suddenly release the sheet it will wobble up and down a bit until it becomes flat again. This is because the surrounding air cannot exert the non-uniform pressure that would be needed to maintain the ripples.
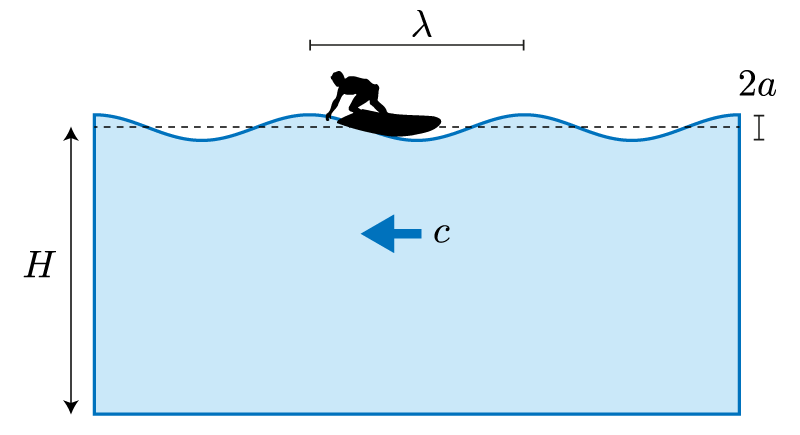
The situation changes if we start moving the (frictionless) rippled sheet with a constant velocity over the water surface. Let's say that we move the sheet to the right with velocity $c$. If we move with the sheet (like the surfer in figure 2) it will appear to us as if the water is moving to the left with velocity $-c$, while the shape of the surface remains stationary.
For the water to follow the crests and troughs in the surface, it has to flow a bit faster than $c$ near the troughs (low parts) and a bit slower near the crests (high parts). Now there is a very useful principle in fluid mechanics, called Bernoulli's principle, which states that, in a steady flow, fluid that speeds up along its way experiences a pressure drop (and vice versa). So as the water is streaming along, the pressure lowers toward the troughs and rises toward the crests, helping us to keep our imaginary sheet deformed. The difference in flow speed in the crests and troughs will be proportional to the horizontal velocity $c$ of the sheet (i.e., the wave speed). So we could try to adjust $c$ in such a way that the resulting Bernoulli pressure exactly balances the hydrostatic pressure from the weight of the water. We can then remove the imaginary sheet and have the disturbance travel on its own, as a wave. In the next section we will play this game in a mathematical way. We will assume that the wave amplitude $a$ remains small with respect to the wavelength $\lambda$ ($a \ll \lambda$) and that the pond is deep ($\lambda \ll H$). This allows for some simplifications in the math, while still capturing many of the essential features.
Wave speed
From the point of view of the surfer the flow is steady (i.e. it does not change in time). We can write the vertical and horizontal velocities at any point $(x, z)$ in the water as
\begin{equation}
v_x = -c + u(x,z) \label{velpert} \\
v_z = w(x,z),
\end{equation}
where $u(x,z)$ and $w(x,z)$ represent small velocity deviations with respect to the main flow ($v_x = -c$, $v_z = 0$). The simplification in what follows consists in keeping only terms which are linear in the perturbations $u$ and $w$, and thus neglecting terms of higher order like $u^2$, $w^2$ and $uw$. This approach, called 'linearization,' is similar to what we used to study the stability of a spinning book.
The derivation of the wave speed can be split up in three steps: (A) First we need to relate $u(x,z)$ and $w(x,z)$ in such a way that the flow satisfies Newton's equations of motion and that at the same time the fluid behaves as if it is incompressible (as water to a good approximation is). (B) We can then solve the resulting partial differential equation for a given wave-like perturbation of the water surface and wave velocity $c$. (C) Finally, we will adjust $c$ to make the pressure at the water surface uniform (corresponding to the uniform outside air pressure). This value of $c$ then corresponds to the actual velocity of the wave (for the given wavelength).
A. Equations of motion
The equations of motion for a (2D) steady fluid flow are:
\begin{equation}
v_x \pd{v_x}{x} + v_z \pd{v_x}{z} = -\frac{1}{\rho} \pd{p}{x} \label{eulereq} \\
v_x \pd{v_z}{x} + v_z \pd{v_z}{z} = -\frac{1}{\rho} \pd{p}{z} - g,
\end{equation}
where $\rho$ is the density of the fluid and $g$ is the gravitational acceleration. These equations represent Newton's $F = ma$ for a continuous flow. In this case the "forces" on the right hand side are pressure gradients and gravity. Viscous effects in the water are neglected here (i.e., friction between parts of the fluid). These effects are only important in a small layer very close to the bottom of the pond (and around the duck) and won't affect the overall flow too much in this case (except for providing some small damping).
So far we have three unknown fields, $v_x(x,z)$, $v_z(x,z)$ and $p(x,z)$, but only two equations. In other words, we need one more equation to "close" the problem. This equation reads
\begin{equation}
\pd{v_x}{x} + \pd{v_z}{z} = 0 \label{incomp},
\end{equation}
which expresses the fact that water is practically incompressible (i.e. if you try to squeeze a piece of water in one direction it will want to flow out into the other directions so that its volume remains the same).
In general this set of equations is very difficult to solve. Mainly because of the non-linear terms on the left hand side in \eqref{eulereq}. However, if we restrict ourselves to waves of small amplitude there is some hope. Substituting our perturbation ansatz \eqref{velpert} into equations \eqref{eulereq} and \eqref{incomp} and keeping only terms linear in $u$ and $w$, we find the following simplified set of equations:
\begin{equation}
-c \pd{u}{x} = -\frac{1}{\rho}\pd{p}{x} \quad \text{(a)} \label{eulerlin}\\
-c \pd{w}{x} = -\frac{1}{\rho}\pd{p}{z} - g \quad \text{(b)} \\
\pd{u}{x} + \pd{w}{z} = 0. \quad \text{(c)}
\end{equation}
Similar to the approach to solve a system of algebraic equations we can now try to substitute one into the other to find a single equations involving only one of the fields. However, since these equations involve some pesky differential operators, we have to be a bit smart about it. In the next section we will see that the boundary conditions are most easily expressed in terms of $w$, so it makes sense to try to single out $w$ first.
The first step is easy: according to (\ref{eulerlin}c) we can replace $\pdi{u}{x}$ in (\ref{eulerlin}a) with $-\pdi{w}{z}$. We now have "used up" (\ref{eulerlin}c) and are left with two equations with two unknowns:
\begin{equation*}
c \pd{w}{z} = -\frac{1}{\rho}\pd{p}{x} \\
-c \pd{w}{x} = -\frac{1}{\rho}\pd{p}{z} - g.
\end{equation*}
Now comes the big trick. In the first equation we take on both sides an additional derivative with respect to $z$, and in the second we do the same, but with respect to $x$. We end up with
\begin{equation*}
c \pd{^2 w}{z^2} = -\frac{1}{\rho}\pd{^2 p}{z \partial x}\\
-c \pd{^2 w}{x^2} = -\frac{1}{\rho}\pd{^2 p}{x \partial z}.
\end{equation*}
If all the functions are nice and smooth (which we will assume), then one can show that $\partial_{z}\partial_{x} p = \partial_{x}\partial_{z} p$ (i.e. the order of taking the derivatives does not matter). By subtracting the second equation from the first we get rid of the pressure term and end up with the equation for $w(x,z)$ we set out for:
\begin{equation}
\pd{^2 w}{x^2} + \pd{^2 w}{z^2} = 0. \label{laplace}
\end{equation}
A physicist immediately recognizes this equation as the famous Laplace equation, which for example also appears in the calculation of the electric potential between charged conductors, or in heat conduction problems. It is one of those few equations physicists know how to solve.
B. Boundary conditions
Although equation \eqref{laplace} limits the number of possible flows, it is still far too general to describe a water wave. The most important additional constraint we have to impose is that the flow follows the rippled surface.
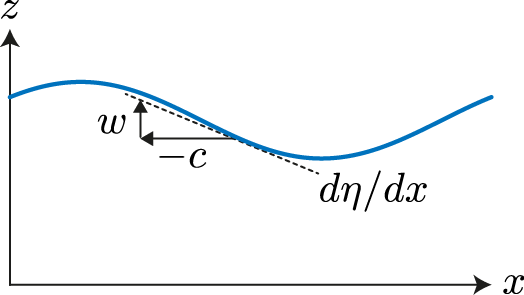
As depicted in figure 3 this means that the vertical velocity component at the water surface ($z \approx 0$) must obey
\begin{equation}
w(x,0) = -c \nd{\eta}{x}, \label{surfbc}
\end{equation}
where the function $\eta(x)$ describes the deviation of the water surface from being flat. The assumption that $\eta$ is small allows us to impose the condition at $z=0$ instead of $z = \eta$, making our live a lot easier.
To proceed, we need to assume a specific wavy (periodic) shape of the surface. It will turn out that a wise choice is
\begin{equation}
\eta(x) = a \cos(k x),\label{waveshape}
\end{equation}
where the so called wavenumber $k$ is directly related to the wavelength $\lambda$ by $k = 2\pi/\lambda$. If we plug this into equation \eqref{surfbc} we find
\begin{equation}
w(x,0) = c\,k\,a \sin(kx).\label{bc1}
\end{equation}
This equation suggests that the full solution, for arbitrary $z$, could look something like
\begin{equation}
w(x,z) = c\,k\,a f(z) \sin(k x),
\end{equation}
where $f(z)$ is some to be determined function of $z$ only that must obey $f(0) = 1$ (to satisfy equation \eqref{bc1}) and $f(-\infty) = 0$ (i.e. there is no velocity perturbation very deep into the pond). Substituting this ansatz into our simplified equation of motion \eqref{laplace} leads to the following ordinary differential equation for $f(z)$:
\begin{equation}
\nd{^2 f}{z^2} - k^2 f = 0.
\end{equation}
As one can easily check, this equation has the following general solution:
\begin{equation}
f(z) = A e^{kz} + Be^{-kz}.
\end{equation}
The constants $A$ and $B$ follow from the conditions $f(0)=1$ and $f(-\infty) = 0$ and are $A = 1$ and $B = 0$. Putting it all together, the full solution for $w(x,z)$ is:
\begin{equation}
w(x,z) = c\, k\, a\, e^{kz} \sin(k x). \label{solw}
\end{equation}
In a similar manner one can figure out the corresponding solutions for $u(x,z)$ and $p(x,z)$. This is left as an exercise for the reader. The final expressions are:
\begin{align}
u(x,z) = c\,k\,a\,e^{kz} \cos(k x) \label{solu} \\
p(x,z) = p_0 + \rho\,c^2\,k\,a\,e^{kz}\cos(kx) - \rho g z. \label{solp}
\end{align}
One can easily check that equations \eqref{solw}, \eqref{solu} and \eqref{solp} represent a correct solution to the (simplified) equations of motion by a direct substitution into equation \eqref{eulerlin}.
C. Matching the uniform air pressure
Now that we know the flow pattern and pressure field for arbitrary $a$, $k$ and $c$, we can try if we can tune $c$ in such a way that the pressure at the surface becomes uniform and matches that in the air. If we evaluate $p(x,z)$ from equation \eqref{solp} at $z = \eta(x) = a \cos(k x)$, we find (to linear order)
\begin{equation}
p_{\eta}(x) = p_0 + \rho a \cos(kx)\left( c^2\,k - g \right),
\end{equation}
From this it is clear that the pressure at the rippled surface can be made uniform (and equal to $p_0$) if we take $c$ to be precisely
\begin{equation}
c(k) = \sqrt{\frac{g}{k}} = \sqrt{\frac{g\lambda}{2\pi}}.\label{disprel}
\end{equation}
This is the so called dispersion relation for (deep) water waves. For a given wavenumber $k$ or wavelength $\lambda$, it tells you the traveling speed of that wave. In this case long waves travel faster than short waves. As we will see later, this special behavior will be essential for understanding the wave patterns behind ducks.
Wave surfers
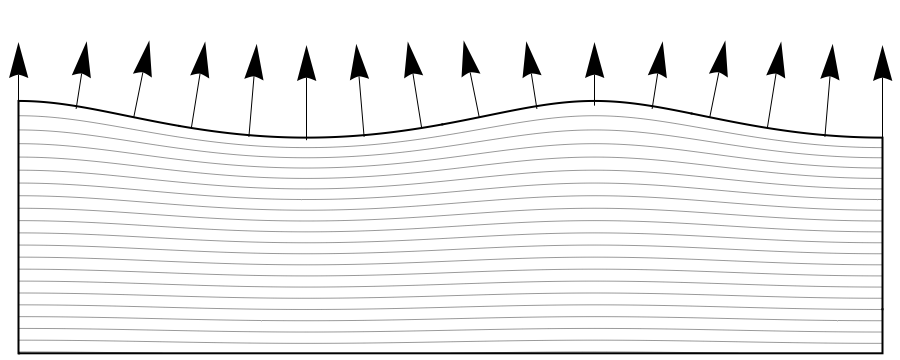
An interesting implication of equation \eqref{solp} is that the buoyancy force at the water surface does no longer point vertically upwards everywhere. Instead, floating objects will experience a force which is perpendicular to the curved water surface (see figure 4). This means that objects floating on the downhill part of the wave will also be pushed forward. In other words, it is possible to surf a wave (which may not come as a complete surprise). Ducks can often be seen to exploit this effect by tagging along in each others wake.
Group velocity versus phase velocity
A swimming duck does not produce a clean wave of a single wavelength. Instead it emits a complicated superposition of waves with slightly different wavelengths. We therefore need to discuss how such groups of waves travel on a water surface.
It may seem that choosing the special waveform given by equation \eqref{waveshape} severely limits the applicability of the previous analysis to the case of the duck. However, our simplified set of equations of motion have the very special property (by design) that they are linear. This means that given two solutions $A$ and $B$, also $C = A + B$ is a solution. By adding the basic form, $a \cos(k (x+\Delta x))$, with different wave numbers $k$, amplitudes $a$ and phase shifts $\Delta x$ we can simulate pretty much any situation we want.
Figure 5 shows what happens when we add two waves of the form $\cos(k x)$ with two slightly different wave numbers, say $k$ and $k+\Delta k$.
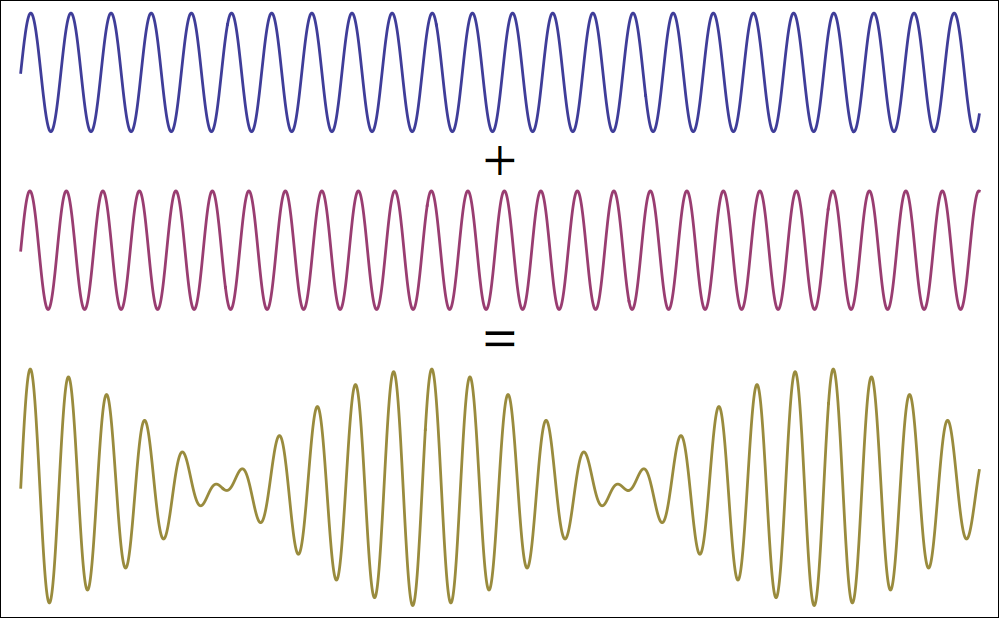
The waveform that emerges is called a 'beat pattern': The short wavelength variations of the initial waves are overlaid with a long wavelength modulation. This modulation occurs because two waves with slightly different wavelengths cannot remain in phase. Periods of constructive and destructive interference take turns.
This behavior can also be made apparent by using a basic relation from trigonometry:
\begin{equation}
\cos(k_1 x) + \cos(k_2 x) = 2\cos\left(\frac{k_1 + k_2}{2}x\right)\cos\left(\frac{k_1-k_2}{2}x\right).
\end{equation}
Setting $k_1 = k+\Delta k$ and $k_2 = k$, and assuming that $\Delta k \ll k$ we find
\begin{equation}
\cos((k + \Delta k) x) + \cos(k x) \approx 2\cos(kx)\cos\left(\frac{\Delta k}{2}x\right). \label{beatx}
\end{equation}
So the wavenumber of the modulation is given by $k_m = \Delta k/2$, or in terms of the wavelength, $\lambda_m = 2\pi/k_m = 4\pi/\Delta k \approx 2\lambda^2/\Delta \lambda$. The smaller the wavelength difference, the longer the wavelength of the modulation.
Guitar tuning
Instead of moving along with the wave, like the surfer, we can also stay on the beach and watch it pass by. In this case the water surface at any fixed point in space moves up and down with a certain frequency (number of up-down-up cycles per second). This frequency can of course be related to the speed of the wave and its wavelength. The time it takes for two crests to pass is equal to $\Delta t = \lambda/c$, so the frequency is $f \equiv 1/\Delta t = c/\lambda$, or, in terms of the wavenumber $k$, $f = c k / (2 \pi)$. To get rid of the annoying $2\pi$ factor it is convenient to convert this frequency to radians per second: $\omega \equiv 2\pi f = ck$. The amplitude of the wave as a function of time will then look something like this:
\begin{equation}
\eta(t) = a \cos(\omega t),
\end{equation}
This form is similar to equation \eqref{waveshape}, with $\omega$ playing the role of $k$ and $t$ playing the role of $x$.
We can now repeat the wave addition game from the previous section in the time domain. If we add two waves which are close in frequency, say $\omega$ and $\omega + \Delta \omega$, we find from equation \eqref{beatx} that:
\begin{equation}
\cos((\omega + \Delta \omega) t) + \cos(\omega t) \approx 2\cos(\omega t)\cos\left(\frac{\Delta \omega}{2}t\right). \label{beatt}
\end{equation}
The closer the two frequencies are, the smaller the frequency of the modulation given by $\omega_m = \Delta \omega / 2$ will be.
The above relations for wave beat patterns are very useful. To give a practical example (this time for sound waves) consider the problem of tuning the strings of a guitar, given that one of the strings is already properly tuned. Let's assume that my d-snare is tuned.
Figure 6 shows a sound recording of me plucking the d-snare. As shown in the magnification in the inset there are approximately 14.7 cycles in 0.1 seconds, so the frequency is approximately $f=14.7/0.1 = 147\,\text{Hz}$, which is indeed what it should be for a d-snare.
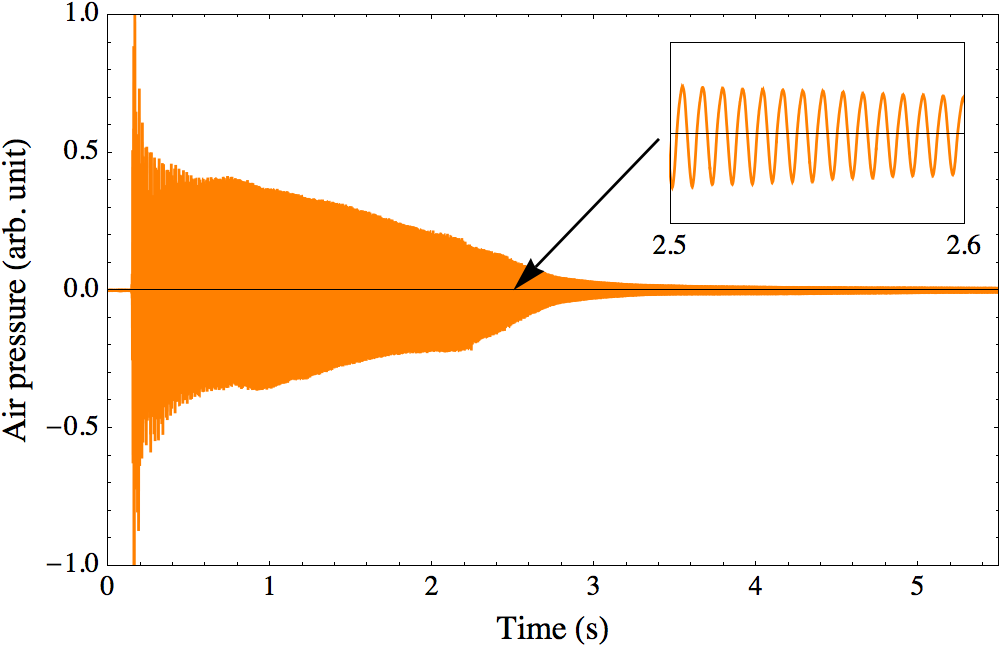
Now suppose we want to tune the a-snare, i.e. one snare up on the guitar. The trick, well known to any guitarist, is that the 5th fret on the a-snare should sound the same as the d-snare. So if we first hit the d-snare and then the a-snare with the 5th fret pressed down, we should hear the same tone. Professional musicians can immediately hear the difference and adjust the tension in the a-string accordingly.
But don't despair, for those among us which are not equipped which such an excellent tone judgment, there is another way. If we hit the two snares at the same time, so that the sounds add up, then according to equation \eqref{beatt} there will be a slow beating pattern if the frequencies do not exactly match. The closer the two frequencies, the slower this beating pattern. Figure 7 shows an example in which the two snares are almost in tune.
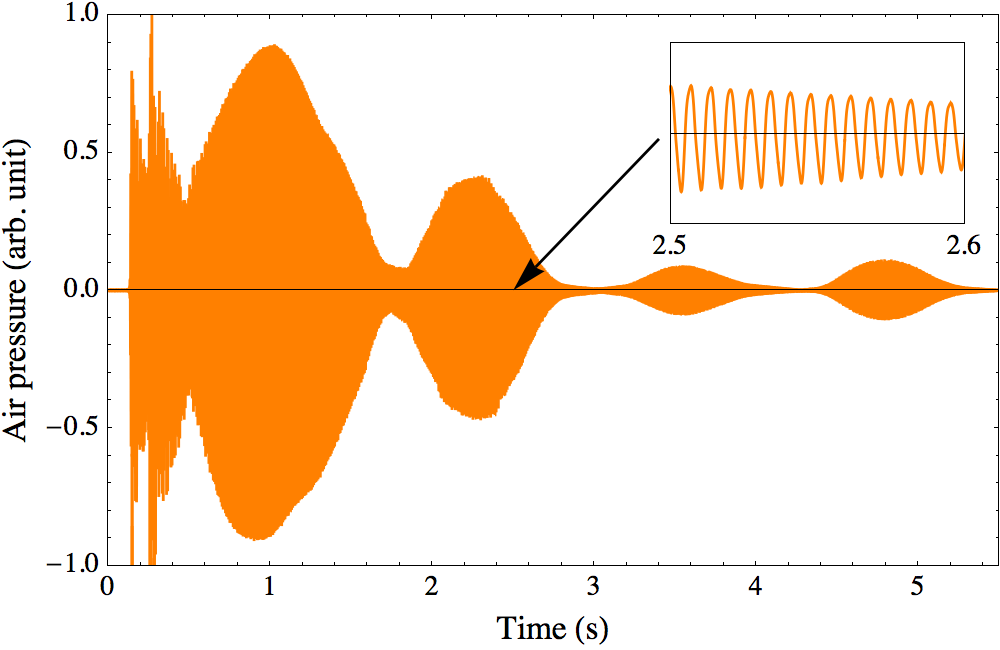
It sounds like a slow hum which repeatedly fades out and then becomes louder again. From the frequency of the hum we can estimate how far the frequencies are apart. There are approximately 3 cycles in 5 seconds, so $\Delta f = 2 \times (3/5) = 1.2\,\text{Hz}$, a relative error of about 1% compared to the frequency of the d-snare. To tune the snares even better we have to minimize the frequency by which the hum becomes louder and softer. This trick can be repeated for every snare, until they are all in tune with each other and with the d-snare.
Waves in space and time; the group velocity
In the previous section we pretended to be watching the wave at one fixed position in the x-coordinate. We can extend this idea to the situation in which many (imaginary) people at different positions along the beach monitor how the wave changes in time. An efficient way to relate the amplitudes observed at all these different positions, is to represent the wave by a single function of both space and time:
\begin{equation}
\eta(x,t) = a \cos( kx \pm \omega t)
\end{equation}
or, by using that $\omega = ck$,
\begin{equation}
\eta(x,t) = a \cos( k(x \pm ct)).
\end{equation}
From this last form it can be clearly seen that the equation represents wave patterns which translate at a uniform speed $c$ to the left (+) or to the right (-).
By now you can probably guess what will be the next step. Yes, we will add two waves which are close in both wavenumber and frequency:
\begin{equation}
\cos((k+\Delta k) x - (w+\Delta \omega) t)) + \cos(k x - \omega t)) \\
\qquad\approx 2 \cos(kx - w t) \cos\left( \frac{\Delta k x - \Delta \omega t}{2}\right) \\
\qquad=2\cos(k(x - c t) \cos\left( \frac{\Delta k}{2}\left( x - \frac{\Delta \omega}{\Delta k} t\right)\right)
\end{equation}
From the last expression we see that the wave is composed of a high wavenumber (i.e. small wavelength) part which travels at the usual wave speed $c$, modulated by a low wavenumber (long wavelength) envelope which travels at a different speed $c_g = \Delta \omega/\Delta k$. Since $\omega$ and $k$ are related through the dispersion relation (equation \eqref{disprel}),
\begin{equation}
\omega(k) = c(k) k = \sqrt{g k},
\end{equation}
also $\Delta k$ and $\Delta \omega$ are related. In fact, for small differences we can write
\begin{equation}
\Delta \omega = \pd{\omega}{k} \Delta k,
\end{equation}
so that the envelope speed, also called the group velocity, becomes
\begin{equation}
c_g = \Delta \omega/\Delta k \approx \pd{\omega}{k} = \frac{1}{2}\sqrt{\frac{g}{k}} = \frac{1}{2}c.
\end{equation}
In other words, for water waves the group speed $c_g$ is one half of the phase speed $c$. An animation of this funny behavior can be seen in figure 8.
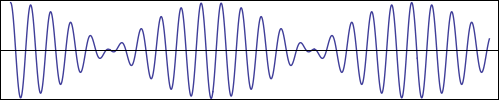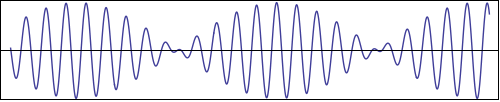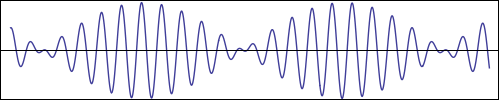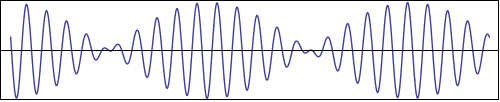
To contrast this with some other common waves: For sound waves the relation between frequency and wavenumber is simply $\omega = c_s k$, where $c_s$ is the (wavelength independent) speed of sound in air. So in this case we find $c_g = \pdi{\omega}{k} = c_s$, which is of course pretty boring. The same holds for light waves, which all travel at "the speed of light". This "boring" character is actually what makes sound and light waves (including radio waves) so well suited for communication purposes (Talking would be a quite interesting experience if different tones traveled at different speeds).
We will soon see that the special property of water waves, that $c_g = c/2$, is the key ingredient to understand the wave patterns behind ducks.
Dispersion
One can argue that the beat pattern discussed above does not really represent a proper group of waves. We added only two waves and the resulting modulated pattern was not confined in space. We can do better!
To construct a wavy pattern with a finite extend in space we can take a basic wave form, say with wavelength $k_0$, and multiply it by a function which quickly goes to zero outside a specified range. A simple function with this property is the bell shaped gaussian curve $g(x) = e^{-x^2/(2\sigma^2)}$, in which $\sigma$ sets the width the bell. So we impose the initial wave pattern to have the following functional form:
\begin{equation}
\eta_0(x) = \cos(k_0 x)\,e^{-\frac{x^2}{2\sigma^2}}.\label{packetform}
\end{equation}
Now you may get discouraged and think that we have to try to solve the equations of motion all over again to see how this new kind of wave form (which is not of our standard form) evolves in time. Luckily, some time back, in 1822, a man called Joseph Fourier discovered one of the most powerful mathematical tricks known to mankind, which will save us a lot of time here. He showed how practically any function can be decomposed in a (infinite) series of cosine and sine functions by properly choosing the amplitudes of the different components. I will spare you the details of how to find these amplitudes here. The final result for our function is:
\begin{equation}
\eta_0(x) \approx \frac{\sqrt{2\pi} \sigma}{L} \sum_{n=-N}^{N} e^{-\frac{1}{2}\sigma^2 (\Delta k_n)^2} \cos((k_0 + \Delta k_n) x),
\end{equation}
where $\Delta k_n = 2\pi n/L$. The number components in the sum, set by $N$, determines the accuracy of the approximation, ideally $N \rightarrow \infty$. The above expression represents the solution in a finite periodic box of length $L$. The solution converges to equation \eqref{packetform} when $L \rightarrow \infty$. In practice $L$ should be taken at least a few times the width $\sigma$ of the wave packet. Notice that the function $a(\Delta k) = e^{-\frac{1}{2}\sigma^2 (\Delta k)^2}$ describing the amplitude of the different wave components has a gaussian form, just like our initial condition. This means that only waves with wave numbers close to $k_0$ contribute significantly to the sum. The range of significant $\Delta k$ (i.e. the width of the gaussian) is inversely proportional the group's width $\sigma$. This is an instance of the so called uncertainty principle for waves. The better the "position" of the wave group is defined, the more "uncertain" is its wave number/wavelength.
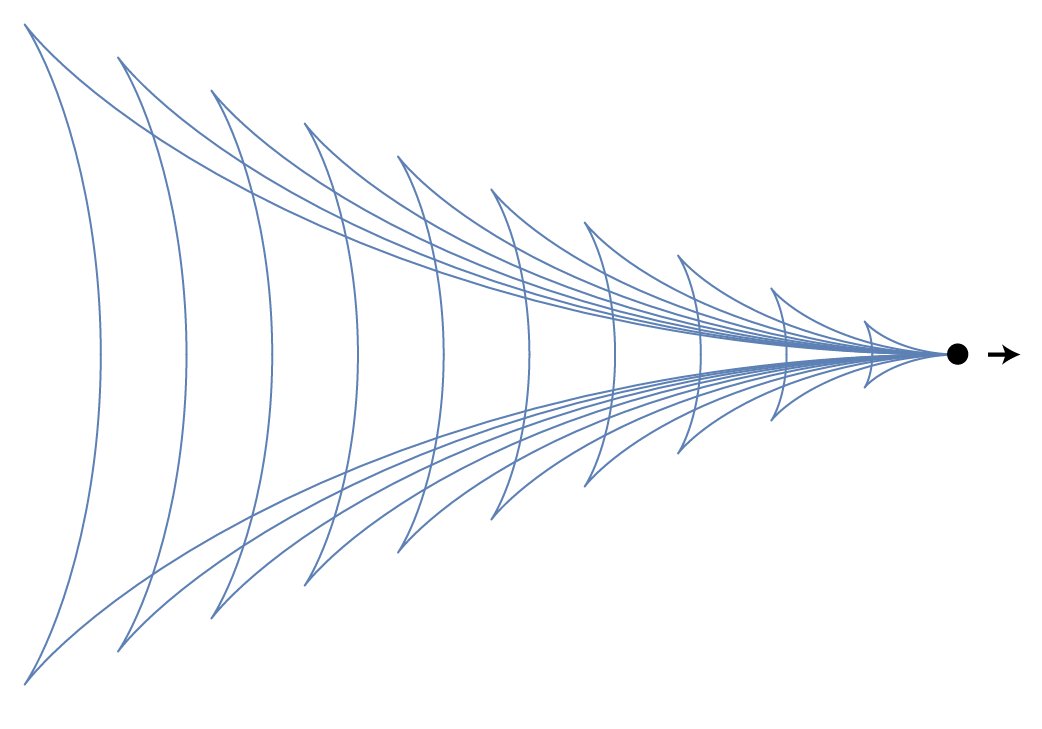
Now that we have represented our initial condition as a sum of basic wave forms it is an easy task to find its full time evolution. Just like we did in the previous section for two waves, we just have to replace each $\cos(k x)$ in the sum by $\cos(k (x - c(k)t))$. Figure 9 shows an animation of the resulting wave evolution.
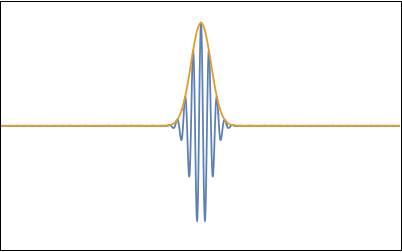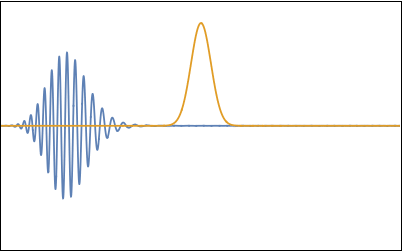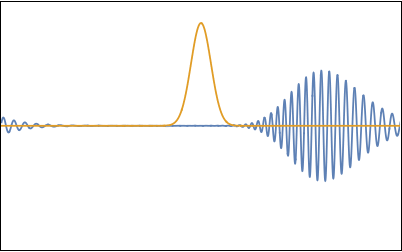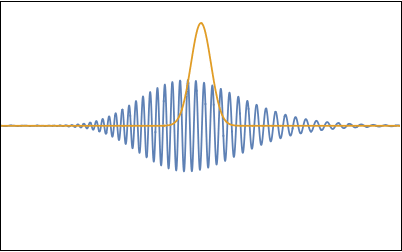
Again the group of waves, also called a 'wave packet', travels at the group speed $c_g$ which, for water waves, is one half the phase velocity of $c_0$ of the "carrier wave" with wavelength $k_0$ (i.e. the crests in the packet travel faster than the packet itself). Additionally we see that the packet broadens in time. This happens because the longer wavelengths in the packet travel somewhat faster than the shorter wavelengths, so that they cannot stay together. If one looks carefully one can see that near the end of the animation the distances between the crests are slightly larger in the front of the packet than in the back. The dispersion rate $\Omega$ of waves is related to the second derivative (with respect to $k$) of the dispersion relation:
\begin{equation}
\Omega(k_0) = \frac{1}{\sigma^2}\left|\pd{^2 \omega}{k^2}\right| = \frac{g^{1/2}}{4\sigma^2|k_0|^{3/2}}.
\end{equation}
The corresponding time evolution of the packet width is
\begin{equation}
\sigma(t) = \sigma\sqrt{1+\Omega(k_0)^2 t^2}.
\end{equation}
For large times the width simply increases linearly in time $\sigma(t) \approx \sigma \Omega t$. In the duck wake one can observe this as a progressive broadening of the "lines" of the V-shape left behind.
Notice that for light and sound waves one has $\pdi{^2 \omega}{k}=0$. These waves show no dispersion and are therefore a lot simpler to deal with. As Richard Feynman puts it in his famous lectures [4]: "[water waves] that are easily seen by everyone and which are usually used as an example of waves in elementary courses [...] are the worst possible example [...]; they have all the complications that waves can have."
Construction of the wake pattern (finally!)
Now that we have a basic understanding of how waves travel on a water surface, we can finally get back to the duck wakes!
The only additional ingredient that we need to construct the wake is the observation that the whole pattern of crests and troughs is stationary with respect to the swimming duck. In other words, if one moves along with the duck, the deformation of the water surface appears frozen in time and space (except for the fact that the wake pattern gets progressively longer, at half the speed of the duck). One says that the phase of the waves is locked to the duck. In general a duck will emit a complicated superposition of waves in all directions and with different amplitudes, but by using this simple principle it is possible to say a whole lot about the overall pattern that will emerge.
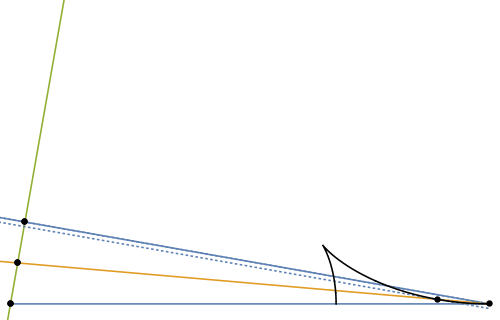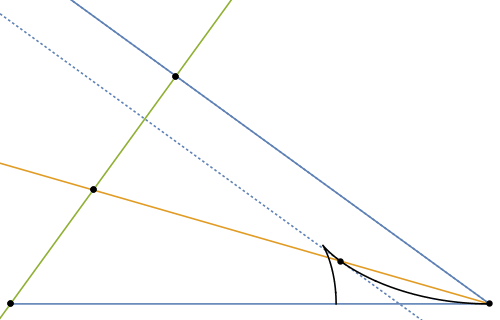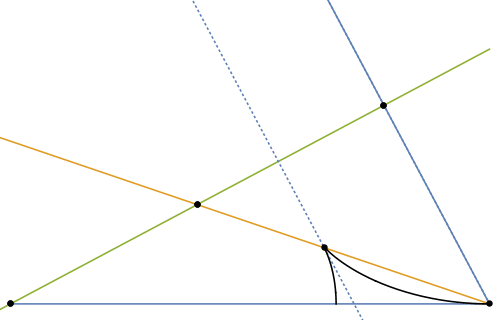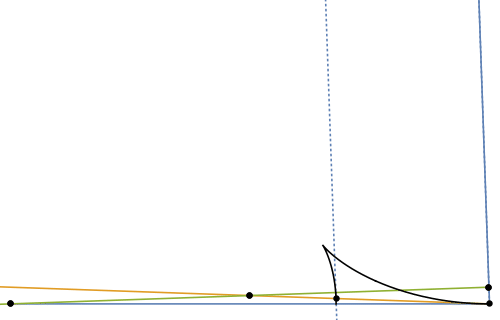
Figure 10 shows the basic geometric construction that we need (which was first introduced in Ref. [2]). It represents a duck that moves from A to B with a certain constant velocity $V_\text{duck}$. We suppose that at point A it has emitted (among others) a wave which travels in the direction AC.
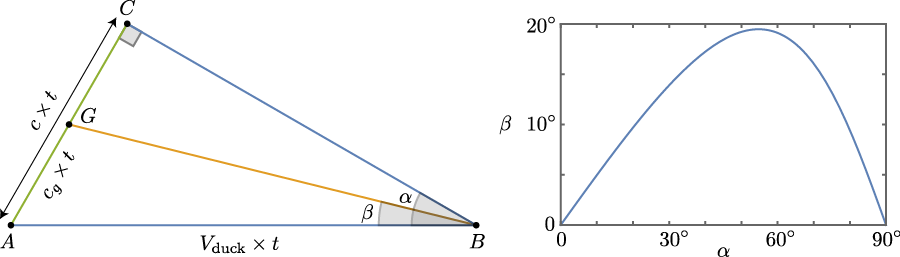
In order for the phase of this wave to keep up with the duck, the wave's phase velocity $c$ projected on AB must be equal to $V_\text{duck}$, thus
\begin{equation}
c(\alpha) = V_\text{duck} \sin(\alpha), \label{phaseproj}
\end{equation}
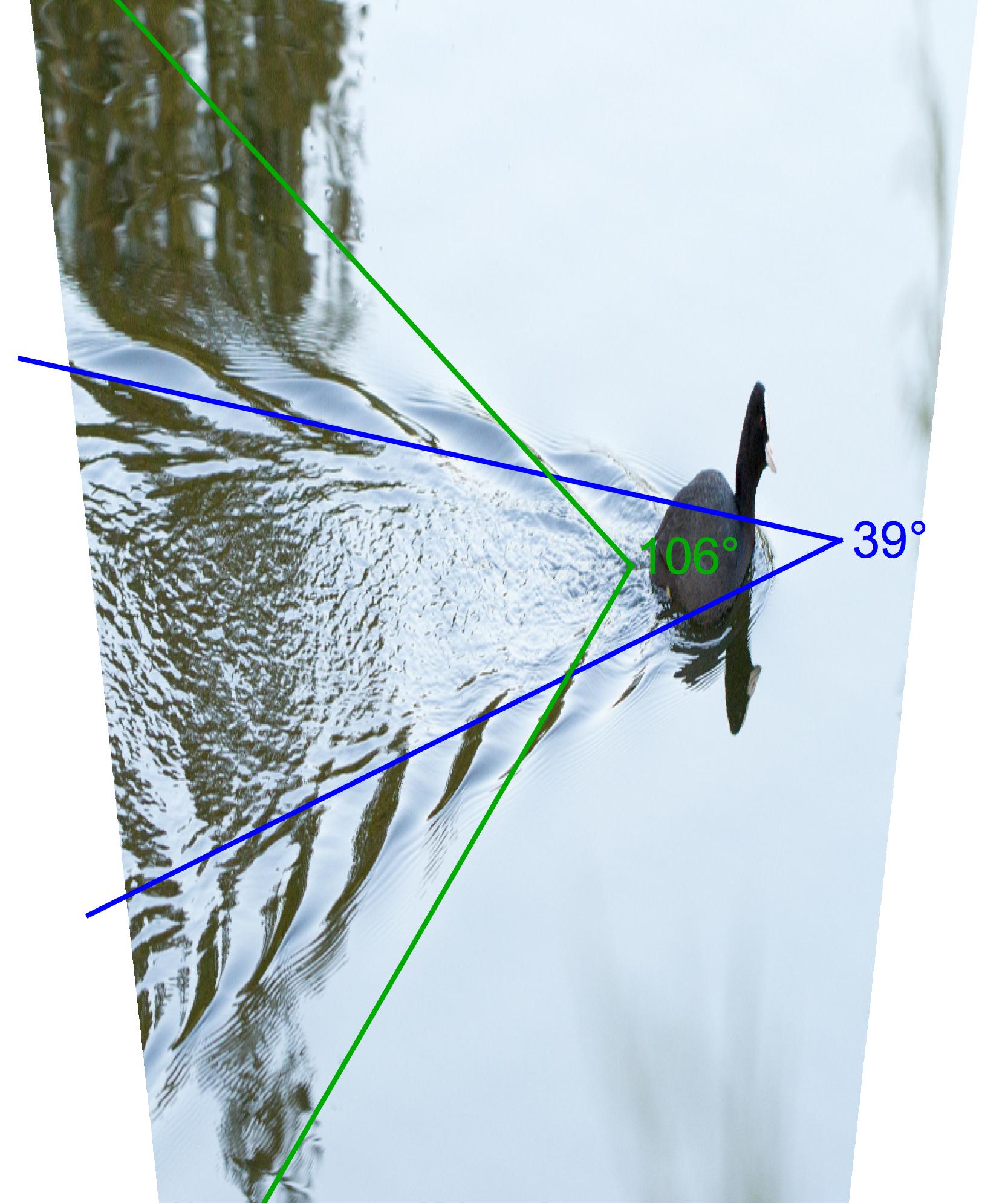
where $\alpha$ is the angle between the wave crests and the swimming direction of the duck (the angle between legs AB and BC in figure 10). Now comes the crux. As outlined in the previous sections, the position around which the emitted waves will be visible is determined by their group velocity, which is one half of the phase velocity. The orange line BG in figure 10 depicts where, for a given group of waves satisfying (approximately) equation \eqref{phaseproj}, the packet of crests and troughs will be visible. The angle $\beta$ between AB and BG varies with the angle $\alpha$. However, as shown in the graph on the right in figure 10, the range of angles where waves are visible is limited. From the geometry it follows that waves are only visible between $\beta = \pm \sin^{-1}(1/3) \approx \pm 19.5^\circ$, independent of the speed of the duck! Similar to what we have seen for light caustics the superposition of waves will give the strongest water disturbance near this extremum, as is clearly visible in the experiment.
We can take the geometrical wake construction one step further and also try to figure out the pattern that the wave crests make on the water surface. For this we need the fact that the spacing between crests (i.e. the wavelength) varies with the wave speed as $\lambda \propto c(\alpha)^2$ (see equation \eqref{disprel}). As shown in figures 11 and 12, the intersection of these crest lines with the group velocity line (where the crests are visible) gives a good impression of the feather-like pattern of waves seen in the duck's wake. A cusp separates the inner 'transverse waves' (with the crests almost perpendicular to the direction of motion) from the 'divergent waves', which form the slanted "feathers" seen at the edge of the wake.
Comparison with experiment
The ultimate test of theory is of course experiment. However, to compare our experiment to the theory set out above we have to take into account that the photo was taken under an angle, while in the theory we obtained the wake pattern as seen from above. We can correct for this difference in perspective by projecting the original photo, which resides in the sensor plane O-y, onto the "pond plane" O-y' (see figure 13).
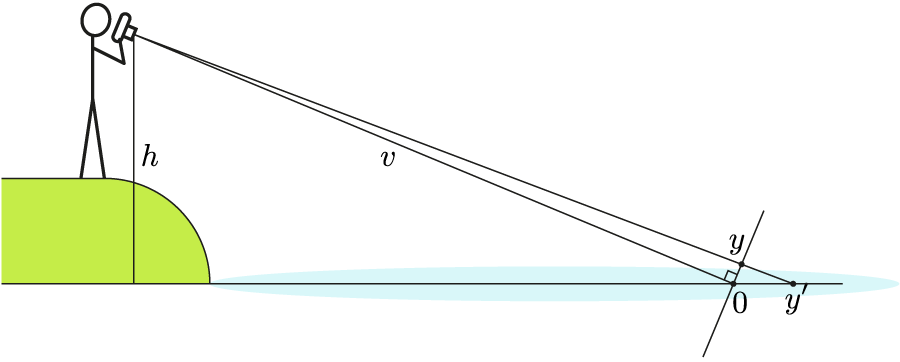
With some geometry one can relate the coordinates in the two planes as follows (where $x$ is the coordinate going into the screen in figure 13):
\begin{align}
y' &= \frac{v y}{h - y\sqrt{1-\frac{h^2}{v^2}}} \\
x' &= \frac{h x}{h - y\sqrt{1-\frac{h^2}{v^2}}}.\label{transform}
\end{align}
To test these relations, I took an angled picture of the square wisdom tile that usually adorns the wall in my bathroom (see figure 14, left). After measuring the distances $h$ and $v$ and the width of the tile (to convert the coordinates in the picture from pixels to meters) I used the function 'ImageForwardTransformation' in Mathematica to transform the coordinates according to equation \eqref{transform}. As evidenced by the neat square tile that emerges from the transformation (figure 14, right) it seems that everything is OK.

In figure 15 I applied the transformation to the picture of the coot. I estimated my height $h$ above the water surface to be about 3 meters; the distance to the duck $v$ was 13.2 meters according to the meta-data saved by the focusing mechanism in my camera; and on Wikipedia one can read that the size of a full grown coot is typically 37 cm, which sets the scale of the picture (this is also consistent with the magnification calculated using $v$ and the focal length of the lens). Given the rough estimates that I had to made, the correspondence between the theory and the experiment seems quite good!
Boats, fish and mosquitoes
Of course not only swimming birds produce wakes. The same Kelvin wake pattern can for example be seen behind boats (going at cruising speed) and fish swimming just below the water surface (see figures 16 and 17 below). The main requirement is that the speed and size of the object producing the wake must fall in a range that ensures that waves of the required wave speeds can be produced [3]. For very small (millimetric) objects going over a water surface also the surface tension of the water starts to play a role, which we neglected in the above derivation. Indeed, a mosquito skating over a water pond produces a very different kind of wake (see figure 18). But this is another story.
I couldn't think of a better way to end this story than with the memorable conclusion of Lord Kelvin himself [1]:
"[...] you can scarcely see the phenomena more beautifully manifested than by a duck and ducklings. A full sized duck has a splendidly shaped body for developing a wave-pattern, and going at good speed it produces on the surface of a pond very nearly the exact pattern of ocean waves. A little duckling going as fast as it can, perhaps about a knot an hour, shows very admirably the capillary waves, differing manifestly from the ocean waves waves formed in the front and at the rear of a larger body moving more rapidly through the open water. I call attention to this, because, having given you perhaps a rather dry statement of scientific facts, if I can say a word that will lead you each to use your eyes in looking at ships, boats, ducks, and ducklings, moving on water at different speeds, and to observe these beautiful phenomena of waves, I think, even were you to remember nothing of this lecture, you would have something to keep in your minds for the rest of your lives."



References
- W. Thomson (Lord Kelvin), On Ship Waves, Proc. Inst. Mech. Eng. 38, pp. 409-434 (1887) (doi)
- F. S. Crawford, Elementary derivation of the wake pattern of a boat, Am. J. Phys. 52, pp. 782-785 (1984) (doi)
- M. Rabaud and F. Moisy, Ship Wakes: Kelvin or Mach Angle?, Phys. Rev. Lett. 110, p. 214503 (2013) (doi)
- R. P. Feynman, R. B. Leighton, and M. Sands, The Feynman Lectures on Physics, Addison-Wesley, Volume I, Chapter 51-4 (1963) (online version)
